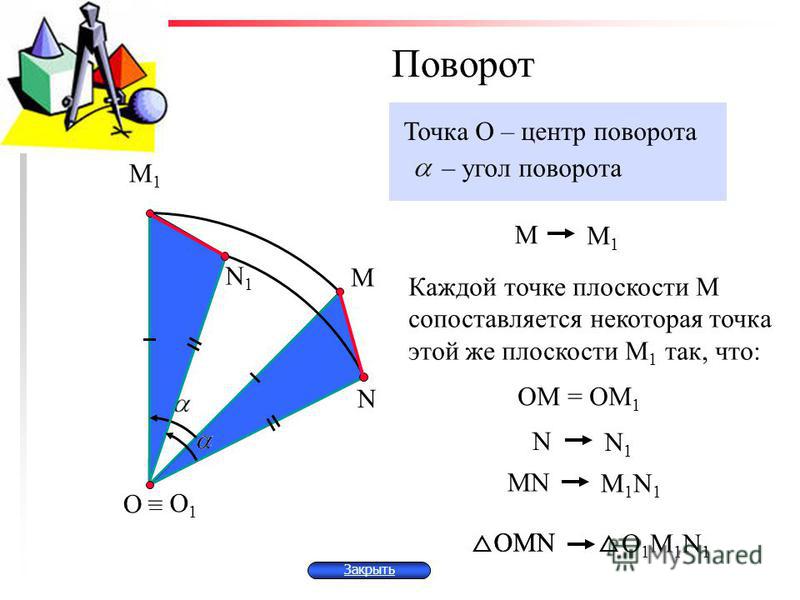
Урок по геометрии по теме «Движение». 9-й класс
Смотрите онлайн или можете скачать на телефон или компьютер в хорошем качестве совешенно бесплатно. Не забывайте оставить комментарий и посмотреть другие фотографии и изображения высокого качества, например Не сложные рисунки в домашних условиях 48 фото и Не сложные рисунки для вышивки крестом 48 фото из раздела Сложные рисунки. Параллельный перенос рисунки сложные фигуры 46 фото. Осевая симметрия. Параллельные фигуры.




![Параллельный перенос рисунки (50 фото) » Рисунки для срисовки и не только Параллельный перенос вектора. Критика [Петр Путенихин] (fb2) читать онлайн](https://i.ytimg.com/vi/Ox5y-dgLFpI/maxresdefault.jpg)







С большим удовольствием "проглотил" очередной том этого замечательного произведения. Фантастики попаданческой ,как и раньше,тут самый мизир. Ну ,небольшие сигналы родне про войну 73 года и Ливанскую гражданскую это почти не в счёт. Зато описание советских реалий начала х выполнено великолепно. Вообще создается у меня впечатление,что мы с автором одними тропками ходили и почти в одно время. Правда институты разные.
- Парадоксы параллельности. Часть 2
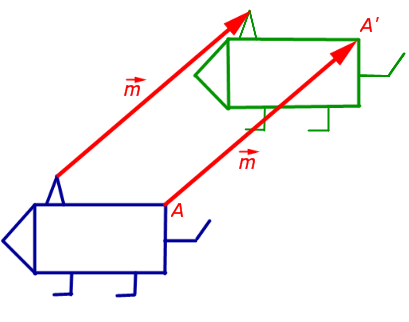
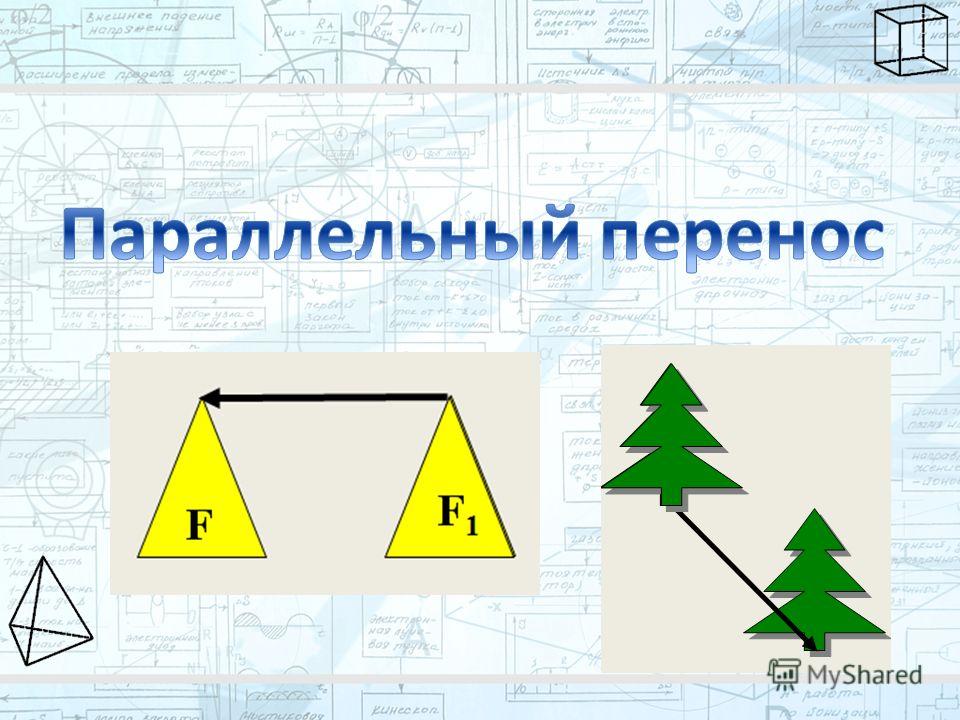
- Введем определение параллельного переноса на вектор. Рисунок 1.
- Все изображения из подборки Идеи для срисовки параллельный перенос можно скачать и просмотреть бесплатно.
- К новогодним праздникам хочется украшать соответствующей атрибутикой не только помещения классов и школьные коридоры, но и общие виртуальные пространства: сайты, блоги, учебные среды. Такого, например: Узор 1.
- Смотрите так же:
- Вход Регистрация.
- К учебнику "Геометрия класс" Л. Атанасян, В.
- Параллельный перенос вектора на сфере с использованием аппроксимированной геодезической.
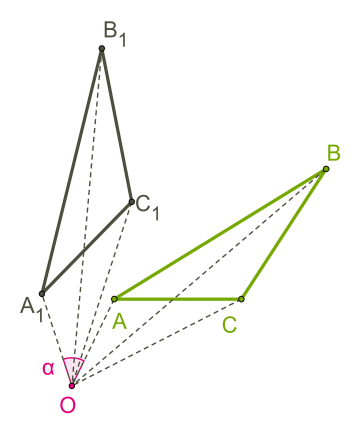
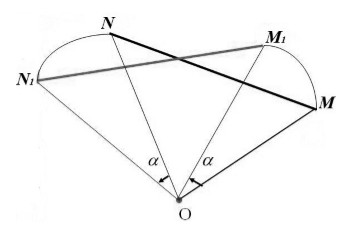






Параллельным переносом называют изменение плоскости со смещением точек в одинаковом направлении на определенное расстояние. Параллельный перенос строго определяют через декартовы координаты или через вектор. Предположим, что на плоскости имеются декартовы координаты х и у. Сформулируем тогда определение параллельного переноса.